Circunferência

Equação reduzida

    Circunferência é o conjunto de todos os pontos de um plano equidistantes de um ponto fixo, desse mesmo plano, denominado centro da circunferência:

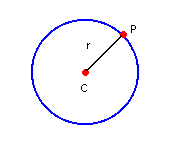
   Assim, sendo C(a, b) o centro e P(x, y) um ponto qualquer da circunferência, a distância de C a P é o raio dessa circunferência. Então:

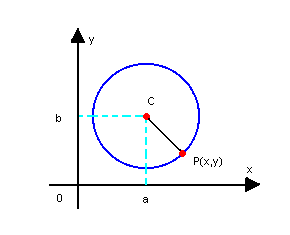
Equação reduzida:  (x - a)² + (y - b)² = r²

Observação: Se o centro da circunferência estiver na origem então a = 0 e b = 0 e teremos:

                       x² + y² = r²

Exemplos:

1) Determinar a equação da circunferência com centro no ponto C ( 4,7) e raio 2.

Temos: a = 4 , b = 7 e r = 2 

           (x - a)² + (y - b)² = r²

      

          ( x - 4 )² +( y - 7)² = 4    

  

2)  Determine a equação da circunferência com centro no ponto C (2, 1) e que passa pelo ponto A (1, 1).

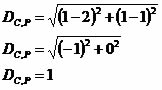
A distância entre o centro C e o ponto P corresponde à medida do raio.

(x – a)² + (y – b)² = R²
(x – 2)² + (y – 1)² = 1²

(x – 2)² + (y – 1)² = 1

3) Determinar as coordenadas do centro C e o raio da circunferência de equação                             
    ( x - 3)² + ( y + 1)² = 16.

 A equação reduzida da circunferência é do tipo  (x – a)² + (y – b)² = R²  assim temos:

 - a = -3 logo a = 3        ;       - b = 1  logo b = -1      e   r² = 16  logo r = 4

Assim: C ( 3, -1)  e r = 4

 Equação geral da circunferência

A equação normal da circunferência é o resultado do desenvolvimento da equação reduzida. Veja:

(x – a)² + (y – b)² = R²

x² – 2ax + a² + y² – 2by + b² = R²

x² – 2ax + a² + y² – 2by + b² – R² = 0

x² + y² – 2ax – 2by + a² + b² – R² = 0

Exemplos:

1) Determinar a equação normal da circunferência de centro C (3, 9) e raio igual a 5.

(x – a)² + (y – b)² = R²
(x – 3)² + (y – 9)² = 5²
x² – 6x + 9 + y² – 18y + 81 – 25 = 0
x² + y² – 6x – 18y + 65 = 0

2) A equação de uma circunferência com centro em C (a,,b) e raio r é x² +y² - 4x - 8y + 19 = 0

                                                                                                                  

– 2a = -4                        -2b = -8                  Dica: a e b é a metade dos coeficientes de x e y trocando o

    a = -4 / -2                      b = -8 / -2                      sinal

    a = 2                              b = 4

e         a² + b² – R² = 19

           2²  + 4² - r ² = 19

            4 + 16 - 19 = r²

                           1 = r²

                            r = 1

 C ( 2,4) e r = 1

Resumo

Distâncias

Equação geral da reta Equação reduzida da reta y = mx +b

Exercícios terceirão

Os exercícios complementares já estão a disposição na página de vocês.

Boletim

Queridos alunos, é muito importante que os pais ou o responsável vá retirar o boletim  neste sábado e converse com os professores. Estamos contando com a presença de vocês e seus pais.
Profª Ursula.

Determinantes

Galera dos 2º anos!

O vídeo sobre determinante já está disponível na página de vocês. Espero que gostem.

Videos 2

Olá 2º Ano!

Videos sobre matrizes estão na página do 2º ano.
Aproveitem!

Videos

 Olá!

Na página dos 3º anos estão dicas de vídeos para reforçar o conteúdo de probabilidade.
Válido para os alunos do professor André e da professora Ursula.

Probabilidade

Experimento aleatório: É todo experimento que, mesmo repetido várias vezes, sob condições semelhantes, apresenta resultados imprevisíveis, dentre os resultados possíveis.

Exemplos: a) Lançamento de um dado.
                 b) Lançamento de uma moeda.
                 c) Loteria de números.
                 d) Extração de uma carta de baralho.
                 e) Abertura de um livro ao acaso para ver o número da página.

Espaço amostral de um experimento aleatório é o conjunto de todos os resultados possíveis desse experimento. Notação: S

Exemplos: No lançamento de um dado, temos S = { 1,2,3,4,5,6}
                 No lançamento de uma moeda, temos S = { cara, coroa}
                 Para o sorteio do primeiro número da Mega-Sena temos S = { 1,2,3,4 ... 60}. E para o sorteio das seis dezenas o espaço amostral será formado por todos os conjuntos de seis dezenas com números distintos de 1 a 60.  Neste caso C60,6 = 50 063 860 resultados possíveis.

Evento é todo subconjunto de um espaço amostral  S de um experimento aleatório.

Exemplos: 1) No  lançamento simultâneo de e um vermelho, determine o espaço amostral e os eventos A: "sair o mesmo número em ambos os dados"; B: " sair soma 7" ; C: "sair soma menor que 5"; D: sair soma maior que 12".

Resolução: Espaço amostral:  S = { (1,1), (1,2), (1,3), (1,4),(1,5),(1,6), (2,1),(2,2),...,(6,5),(6,6) }
                 Evento A : sair o mesmo número em ambos os dados.  A = {(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)}
                 Evento B : sair soma 7. B = { (1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}
                 Evento C:  sair soma menor que 5. C = {(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)}
                 Evento D:  sair soma maior que 12. D = Ø   (vazio)

                 2) Uma caixa contém 20 bolas de mesmo peso e tamanho numeradas de 1 a 20. Uma pessoa com os olhos vendados, retira uma bola dessa caixa. Determine o evento A:a bola sorteada contém um múltiplo de 4 e o número de elementos deste evento.
                   
Resolução:  A = { 4, 8, 12, 16, 20 }  e n( A) = 5

Observação: n(E) = número de elementos do evento

Evento Complementar

Chamamos evento complementar de E , em relação a S ( espaço amostral) o evento que ocorre quando E não ocorre. Indica-se por  E^C 

Note que: E U E^C = S e  E ∩ E^C = Ø

Exemplo: No lançamento de um dado, observando o número da face superior, podemos descrever o evento A : obter um número ímpar.

Temos : A = { 1, 3, 5 } 

 Logo:  A^c = { 2, 4, 6}

                                                        Exercícios

1) Um dado é lançado e o número da face voltada para cima é anotado.
     a) Descreva S
     b) Qual é o evento A " o número obtido é múltiplo de 3?
     c) Qual é o evento B "o número obtido não é primo" ?

2) A confederação Brasileira de Futebol ( CBF ) realizou um sorteio para decidir em qual região do país seria disputado um torneio internacional. Determine o espaço amostral desse experimento.

3) Uma moeda é lançada duas vezes sucessivamente e observa-se a sequência de faces obtidas. Determine:
     a) S ( espaço amostral)
     b) o evento E "ocorre ao menos uma cara"

4) Um número natural de 1 a 100 é escolhido ao acaso. Seja o evento E "ocorre um número que é uma potência de base 2".
     a) Determine E
     b) Qual é o número de elementos de  E^C

5) Um dado é lançado duas vezes, sucessivamente. Seja o evento E: " a soma dos pontos obtidos é menor ou igual a 9". Determine E^C

6) Um experimento aleatório é composto de duas etapas: primeiro, uma moeda é lançada e, em seguida, um dado é lançado. Construa o espaço amostral desse experimento, utilizando a representação K: cara e C: coroa.

             

Permutação Simples

É o tipo de agrupamento ordenado, sem repetição, em que entram todos os elementos em cada grupo.

A permutação é um caso particular do arranjo, isto é , quando n = p. 

Fórmula da permutação:  Pn  = n !

Exemplos:

1)  Quantos números de 4 algarismos distintos podem ser formados, usando-se os algarismos 1, 3, 5 e 7?

                  A4,4 ou P4 = 4 ! = 4 . 3. 2 . 1 = 24

2) Quantos anagramas tem a  palavra  MITOS ?

     P5 = 5 ! = 120

3) Com relação aos anagramas da palavra ESCOLA, qual o número:

a) total deles?

b) dos que começam com consoante?

c) dos que começam e terminam com vogal?

d) dos que mantêm as letras E, S, A juntas e nessa ordem ?

e) dos que mantêm as vogais juntas?

Resolução:

a) Cada anagrama é uma permutação simples das letras E, S, C, O, L, A
    Logo, a resposta é P6 = 6! = 720

b) Nesse caso, temos anagrama que começam com S, C ou L. Em cada um deles basta permutar as 5 letras restantes.

       3 . P5 = 3 . 5! = 3 . 120 = 360
 =
c) São anagramas do tipo  vogal  . ____  _____  _____  _____ vogal
    Para preencher as extremidades temos os elementos E, O, A ;  logo, há 3 possibilidades de vogais para iniciar e duas para terminar e podemos preencher as posições retantes com as 4 letras que sobraram.
Logo a resposta é:  3 . 2 . 4! = 3 . 2 . 24 = 144.

d) O bloco ESA funciona como se fosse um elemento ( considero como uma letra apenas); basta, então,  permutar os elementos ESA , C, O, L

Logo a resposta é 4! = 24

e)  Cada bloco formado pelas vogais ( por exemplo, EOA ) funciona como um elemento e para cada bloco, temos P4  ( igual ao item anterior). Como não foi dado a ordem, significa que as letras que compõem o bloco podem permutar entre si.

Logo P4 . P3 = 4! . 3 ! = 24 . 6 = 144

Tente você!

Em relação aos anagramas da palavra VISTA, qual é o número:

a) total deles?
b) dos que começam com T ?
c) dos que terminam com vogal?
d) dos que contêm as letras IA juntas e nessa ordem?
e) dos que mantêm as vogais juntas?

Vídeo sobre análise combinatória ( fatorial e combinação)

http://youtu.be/7egxgnVeGKY

http://www.youtube.com/watch?v=fK_v-hyMrUo